An Introduction to Solitons

- Integrability: Before the discovery of solitons, mathematicians and people who used math were under the impression that we could not solve nonlinear partial differential equations...not exactly anyway. However, solitons led us to recognize that through a combination of such diverse subjects as quantum physics and algebraic geometry, we can actually solve some nonlinear equations exactly, which gives us a tremendous "window" into what is possible in nonlinearity.
- Nonlinear Superposition: In linear equations there is a simple way to make new solutions from known ones, just multiply them by scalars and add! This is known as superposition. Before the discovery of solitons, there was no analogue of this construction for nonlinear equations, but the way that a 2-soliton solution can be viewed as a combination (though not a simple linear combination) of two 1-soliton solutions leads to a recognition that (at least for soliton equations) there is a nonlinear superposition principle as well. (This is now understood algebraically in terms of the symmetries known as Darboux-Backlund transformations and geometrically in terms of the structure of the Sato Grassmannian.)
- Particle-like behavior: The particle like behavior of solitons (that they are localized and preserved under collisions) leads to a large number of applications for solitons. On the one hand, we hope to be able to use solitons to better understand real particles. This is already true to some extent: there are soliton models of nuclei and the technique known as bosonization allows us to view particles like electrons and positrons as being solitons in appropriate situations. However, there is so far no general theory in which particles are described as solitons. Still, there are macroscopic phenomena, such as internal waves on the ocean, spontaneous transparency, and the behavior of light in fiber optic cable just to name a few, which are know understood in terms of solitons.
- Algebraic-Geometry: Perhaps the most surprising thing about solitons is the way they combine the subjects of differential equations and algebraic geometry. This has been used to the benefit of each subject. For example, there are large classes of solutions to soliton equations that we know only because they are provided by classical results in algebraic geometry. (In particular, solutions can be written in terms of the theta function of complex projective algebraic curves.) In the other direction, the KP hierarchy of soliton equations provides the only known method for determining whether a given abelian variety is a jacobian variety (a problem known as the Schottky problem in algebraic geometry). Most interesting to me is the way that algebraic varieties play a role for solitons analogous to a vector space in the case of linear equations. In particular, just as the linear combinations of a set of known solutions form a vector space, the "nonlinear superpositions" of solutions to the KP hierarchy form an infinite dimensional grassmannian manifold!
- Books:
 There are many books on soliton theory, although most of them are written for graduate students or researchers. Here are a few suggestions for readers who do not have the training required to read those more advanced books.
There are many books on soliton theory, although most of them are written for graduate students or researchers. Here are a few suggestions for readers who do not have the training required to read those more advanced books.
For a book which focuses on the people and ideas without involving much explicit mathematics or physics, I strongly recommend Filippov's The Versatile Soliton. My own textbook, Glimpses of Soliton Theory (see book cover shown at right) focuses on the underlying mathematical structure of soliton equations, but is written so that it would be understandable to anyone who has taken basic undergraduate courses in calculus and linear algebra. Another good book for undergraduates is Solitons: An Introduction by Drazin and Johnson, which concentrates on solving the PDEs rather than than on understanding their structure, and requires that the reader has some prior experience with differential equations and physics. Finally, for the experimentalists out there, I would recommend Waves Called Solitons: Concepts and Experiments by Michel Remoissenet as a book that addresses solitons as something you can see in a laboratory rather than as abstract objects.
- The Latest Research: For some recent research articles on solitons, click here or here.
- History: For the "story" of the first scientific observation of a soliton in the 19th century (by J.S. Russell) and photographs of a recreation of that event, look here.
The first equation known to admit soliton solutions was the KdV equation. Learn a little about it's history here.
- Applications: Three dimensional solitons in an electromagnetic field are called LIGHT BULLETS. Learn about them here.
An important two dimensional version of the KdV equation (capable of modeling waves on a surface, such as ocean waves) is the the KP equation.
Telecommunications companies use solitons of light to transmit phone signals. See, for instance, here and here.
- A Model of Soliton Stability: Learn about the soliton model
in this picture:

- Check out also the Soliton Gallery in Japan.
|
Technically, a soliton is "a permanent localized disturbance in a non-linear wave". To put it in terms that may be easier to understand, solitons are waves that act like particles. (See
the examples in the pictures below.) It is interesting that such
things exist at all. People once doubted their existence. However,
the mathematical theory of solitons is now a well developed "science".
Solitons have practical applications and they are also interesting
subjects of theoretical study.
Four interesting (and surprising things) about solitons are:
|
An Explicit Example: The KdV 2-Soliton Collision
Let's get specific, and I think it will be easier to see what I mean. The KdV equation is a non-linear partial differential equation for a function u(x,t). If we think of the function of giving the height of the wave at time t and position x along a canal, then this equation does a pretty good job of describing what happens to the surface waves that you can see moving or rippling along the canal. In fact, that was what it was originally derived to do. The KdV equation looks like this: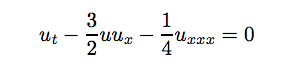
One such solution is the one-soliton given by this formula:
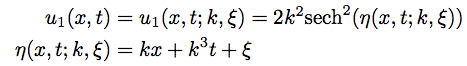
But, that's not the interesting part! The interesting thing happens when you get two of these things travelling at different speeds and you put them together. Of course, you can't just add them, because that would not give you another solution to the equation. But you can check for yourself that if k1 is a real number less than k2 then
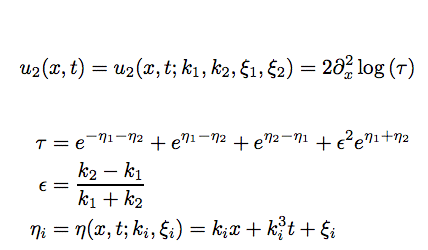
Here's a movie (where each frame of the movie comes from a different value of t) showing what this 2-soliton solution looks like as the two humps meet.
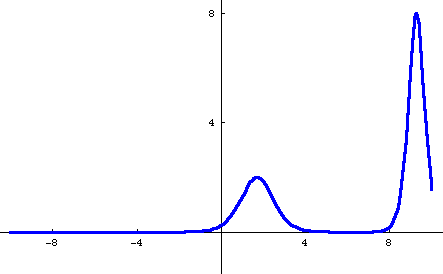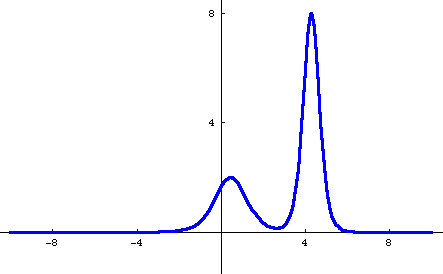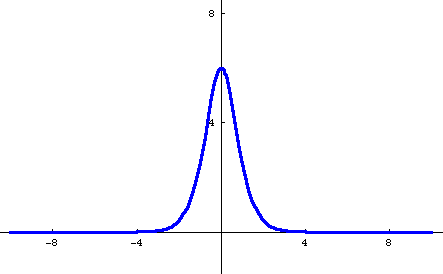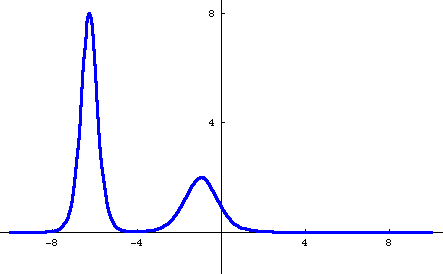
Perhaps you can also notice that the smaller hump after the collision is a little bit shifted back from where you'd expect it to be if it was just going ahead without noticing the other one. (This may be easier to see in the 3D animation at the top of the page.) In particular, notice that after the collision it seems to still be in the same place as before. Similarly, the taller hump is shifted a bit ahead. This "phase shift" is a standard feature of soliton interactions.
Okay, so we know what is not going on. It is not just a sum of the two 1-soliton solutions. But what is going on?
One way to try to understand the interaction is to decompose the two solution u2 into a sum of functions each of which has a "quasi-particle" like behavior. Unfortunately, there is not a unique way to do this and so there is no one answer, but here is my favorite example to show you what I mean. In our paper (On Decompositions of the KdV 2-Soliton, Journal of Nonlinear Science 16/2 2006 pp. 179-200) we show that if you let
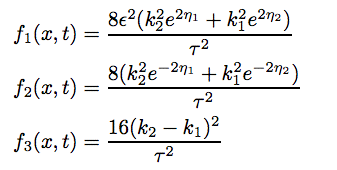
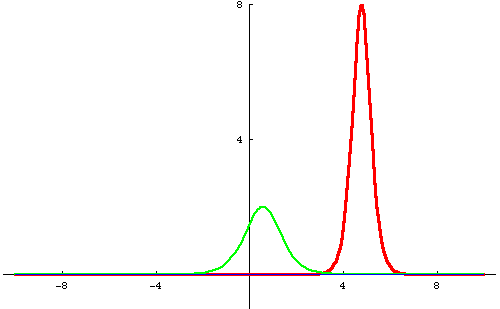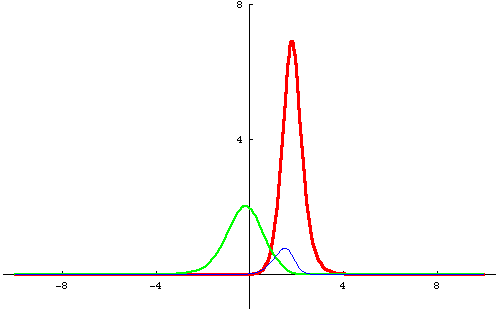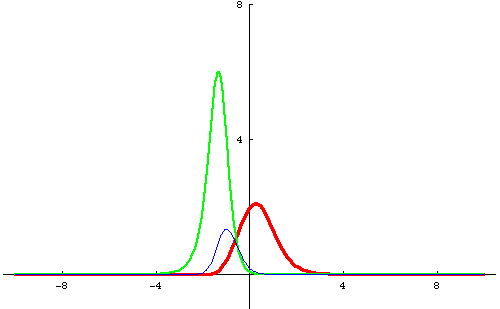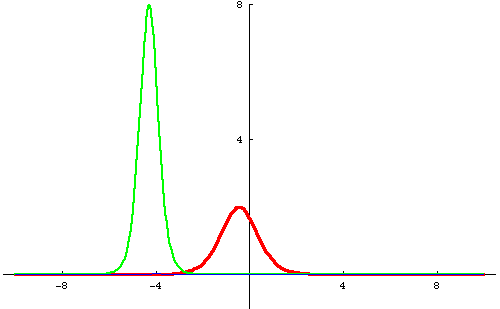
Please read our paper (On Decompositions of the KdV 2-Soliton, Journal of Nonlinear Science 16/2 2006 pp. 179-200) for more information about this decomposition and other decompositions of KdV 2-soliton solutions with interesting properties. It is available from the journal or here in preprint form.
Further Reading
Return to my home page
(If you wish to use the images on this page for some other purpose, please send me a request. Thanks.)